Umíte pascalsky - 28.lekce ...

Umíte pascalsky?
28.lekce
 Vytisknout  
Numerické řešení rovnice s jednou neznámou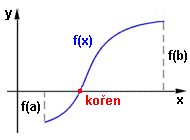

Nechť f(x) = 0 je rovnice s neznámou x. Kořenem rovnice je graficky x-ová souřadnice průsečíku grafu funkce f(x) s osou x.
Určit takto kořen je sice názorné, ale nepřesné a pomalé. Vyjádřit kořen přesně vzorcem lze pouze ve speciálních případech - lineární, kvadratická, kubická, bikvadratická rovnice. Ve většině případů řešíme numerickými metodami.

Při numerickím řešení rovnice o jedné neznámé, tedy F(x) = 0, se ke skutečné hodnotě kořenu rovnice postupně přibližujeme. Většinou ji však nedosáhneme, ale teoreticky se k ní můžeme přiblížit a libovolnou přesností, kterou předem určíme.
Každá numerická metoda vychází z určitého počatečního řešení, které je postupně upřesňováno.

Počateční řešení může být zadáno:
A) intervalem, v němž leží hledaný kořen
B) přibližnou hodnotou kořene

A) Počáteční řešení je zadáno intervalem, v němž leží hledaný kořen

Toto je situace podobná vyhledávání prvku v poli - prvek ale neznáme. Je však dána funkce a přesnost, s kterou kořen hledáme. Lze použít např. jednoduché numerické řešení, půlení intervalu nebo metodu sečen.

1.Jednoduché numerické řešení

Nechť je dána rovnice f(x) = 0 , má kořen v intervalu <a,b> a funkce f(x) je v intervalu <a,b> spojitá (viz obrázek).
Platí-li pro funkční hodnoty v krajních bodech intervalu f(a).f(b) < 0 (mají-li opačná znaménka - graf přechází z jedné strany osy x na druhou), musí mít rovnice v tomto intervalu alespoň jeden kořen (graf musí protínat osu x).
Tento průsečík je skutečnou hodnotou kořenu (kořen).

Máme-li určit aproximaci kořenu s danou přesností, tedy určit přibližnou hodnotu kořene (x_pribl) s danou přesností (presnost), musí platit |x_pribl - koren| < presnost (liší se o presnost).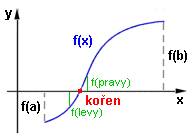

Interval <a,b> rozdělíme na dílčí intervaly <levy,pravy> o délce presnost.
Skutečný kořen bude ležet v tom z nich, u kterého budou funkční hodnoty v krajních bodech levy, pravy opačného znaménka (tedy f(levy).f(pravy) < 0) nebo bude jedna z těchto hodnot rovna nule (tedy f(levy).f(pravy)=0) - trefili jsme do kořene.

Myšlenka (hrubý algoritmus):
<začni prvním dílčím intervalem (levy,pravy)>
dokud f(levy).f(pravy) > 0
  <přejdi na další dílčí interval - posuň o presnost>
x_pribl := <střed naposled uvažovaného dílčího intervalu>

Tato metoda je pomalá, ale lze ji zase použít vždy a lze určit všechny kořeny. Proto se používá jako první (s malou přesností) pro zjištění počtu kořenů a intervalů, kde se nachází (viz domácí úkol). Potom na tento interval použijeme větší přesnost a jinou, efektivnější metodu.

2.Bisekce (půlení intervalu)

Pokud má rovnice f(x) = 0 v intervalu (a,b) jeden kořen, lze ho nalézt rychleji bisekcí.

Interval (levy,pravy) - poprvé to bude (a,b) - rozdělíme na poloviny pomocí středu Stred. Hodnota f(Stred) je buď nula (trefili jsme kořen) nebo má stejné znaménko jako f(levy) nebo f(pravy). Kořen leží v tom intervalu (levy,Stred), resp.(Stred,pravy), jehož hodnoty v krajních bodech mají opačná znaménka (jejich součin je záporný).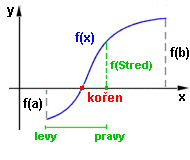

S tímto intervalem pokračujeme v dělení tak dlouho, dokud netrefíme kořen (|f(Stred)|<presnost - hodnota fce je nula s danou přesností) nebo bude délka intervalu menší než přesnost. Střed tohoto intervalu bude přibližná hodnota kořenu x_pribl.

Myšlenka (hrubý algoritmus):
<začni daným intervalem (a,b)>
opakuj
  <vypočti délku intervalu>
  <vypočti Stred intervalu>
  <vyber polovinu s opač.znaménky>
dokud nebude (delka<presnost) nebo (stred netrefil kořen)
x_pribl := <střed naposled uvažovaného intervalu>

3.Regula falsi (metoda sečen)

Interval nedělí na poloviny, ale dělí je pomocí průsečíku Prus sečny s osou x vedenou krajními body intervalu. Z těchto dvou intervalů (levy,Prus), (Prus,pravy) opět vybereme podle znamének funkce v krajních bodech nový interval (levy,pravy). Najdeme průsečík a pokračujeme tak dlouho, dokud nebude průsečík aproximací kořene nebo délka intervalu nebude menší než přesnost.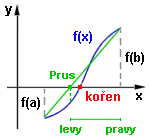

Výpočet průsečíku:
Sečna je určena body o souřadnicích [levy,f(levy)] , [pravy,f(pravy)].
Směrnice sečny bude k = (f(pravy)-f(levy))/(pravy-levy)
a rovnice sečny y - f(levy) = (f(pravy)-f(levy))/(pravy-levy)(x-levy)
Pro průsečík s osou x (y=0) dostáváme Prus = levy - f(levy)(pravy-levy)/(f(pravy)-f(levy))

Myšlenka (hrubý algoritmus):
<začni daným intervalem (a,b)>
opakuj
  <vypočti délku intervalu>
  <vypočti průsečík sečny s osou x>
  <vyber interval s opač.znaménky>
dokud nebude (delka<presnost) nebo (průsečík netrefil kořen)
x_pribl := <střed naposled uvažovaného intervalu>

B) Počáteční řešení je zadáno přibližnou hodnotou kořenu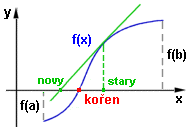

Zde si ukážeme pouze metodu tečen.

4.Newtonova metoda (metoda tečen)

Počátečním kořenem (stary) je střed intervalu (a,b). V tomto bodě sestrojíme tečnu a její průsečík (novy) s osou x je novým přiblížením (aproximací) kořene rovnice. V tomto bodě (teď už bude jako stary) sestrojíme tečnu a určíme její průsečík (novy) s osou x atd. Pokračujeme tak dlouho, dokud se neliší (v absolutní hodnotě) poslední aproximace o méně než přesnost.

Výpočet průsečíku:
Provedete obdobně jako v metodě sečen.

Myšlenka (hrubý algoritmus):
Provedete obdobně jako v metodě sečen.

Příklad: Sestavte program Rovnice pro numerické řešení rovnic s jednou neznámou. Procedura Zadani umožní zadat přesnost řešení a interval obsahující kořen a procedury Jednoducha, Puleni, Secny pro řešení rovnice jednoduchou numerickou metodou a metodami bisekce a regula falsi podle volby uživatele.

Pomocí programu Rovnice určete kořeny rovnic s přesností 0.01 a 0.00001
x3+x2-37x+35=0 v intervalu (-8,6) ... tři kořeny
2sinx + cosx = 2 v intervalu (0,1) ... jeden kořen
lnx - 3 = p v intervalu (400,500) ... jeden kořen

Program Rovice může vypadat takto:

program Rovnice;
  var x_pribl,levy,pravy,presnost,a,b:real;
           volba:integer;
 {proměnné pro kořen,meze intervalu a přesnost}
{volba metody}
 
function Fce(x:real):real;
  begin
     Fce:=x*x*x+x*x-37*x+35;
 {levá strana rovnice f(x)=0}
  end;
procedure Zadani;
  begin
    writeln('Presnost:');readln(presnost);
    writeln('Dolní mez:');readln(a);
    writeln('Horní mez:');readln(b); 		{zadání přesnosti}
{zadání dolní meze}
{zadání horní meze}
  end;

procedure Jednoducha;
  begin
    levy:=a; pravy:=a+presnost;
    while (Fce(levy)*Fce(pravy)>0) do
      begin
        levy:=pravy;
        pravy:=pravy+presnost;
      end;
    x_pribl:=(levy+pravy)/2;
    writeln('Korenem rovnice je x=',x_pribl);
{první interval délky presnost}
{dokud graf nepřechází osu x}

{posun na další interval}

{přibližný kořen uprostřed}
{tisk výsledku}
  end;

procedure Puleni;
  var stred,delka:real;
  begin
    levy:=a;pravy:=b;
    repeat
      delka:=abs(pravy-levy);
      stred:=(levy+pravy)/2;
      if Fce(stred)*Fce(levy)<0 then
          pravy:=stred
        else
          levy:=stred;
    until ((delka<presnost) or (abs(Fce(stred))<presnost));
    x_pribl:=stred;
    writeln('Korenem rovnice je x=',x_pribl);
 {první interval}
{opakuj činnost}
{výpočet délky intervalu}
{výpočet středu intervalu}
{určení nového intervalu}
{přechází osu x vlevo od středu}

{přechází osu x vpravo od středu}
{interval kratší než přesnost nebo trefa do kořenu}
{přibližný kořen je střed}
{tisk výsledku}
  end;

procedure Secny;
  var prusecik,delka:real;
  begin
    levy:=a;pravy:=b;
    repeat
      delka:=abs(pravy-levy);
      prusecik:=levy-Fce(levy)*((pravy-levy)/(Fce(pravy)-Fce(levy)));
      if Fce(prusecik)*Fce(levy)<0 then
          pravy:=prusecik
        else
          levy:=prusecik;
    until ((delka<presnost) or (abs(Fce(prusecik))<presnost));
    x_pribl:=prusecik;
    writeln('Korenem rovnice je x=',x_pribl);
 {první interval}
{opakuj činnost}
{výpočet délky intervalu}
{výpočet průsečíku sečny s osou x}
{určení nového intervalu}
{přechází osu x vlevo od průsečíku}

{přechází osu x vpravo od průsečíku}
{interval kratší než přesnost nebo trefa do kořenu}
{přibližný kořen je průsečík}
{tisk výsledku}
  end;

Begin
   writeln('Program vypočítá existující kořen rovnice Fce(x) = 0 ');
   writeln('s danou přesností v daném intervalu');
   repeat
     Zadani;
     writeln('Vyberte si metodu:');
     writeln('1...jednoducha');
     writeln('2...puleni');
     writeln('3...secny');
     writeln('0...konec');
     readln(volba);
     case volba of
       1: Jednoducha;
       2: Puleni;
       3: Secny;
       0: ;
     end;
   until volba=0;
 {zadání přesnosti a intervalu}

{volba metody}
End.


Domácí úkol:

    Doplňte program Rovnice o volby Pruzkum pro nalezeni všech kořenů rovnice v zadaném intervalu jednoduchou metodou (pokud neexistuje žádný kořen, podat zprávu) a Newton pro nalezení kořenu metodou tečen. Vyzkoušejte na několika rovnicích (polynomická,goniometrická,exponenciální,...) nejprve metodu Pruzkum (s malou přesností) a potom upřesněte (použijte větší přesnost) aplikací metody Newtonovu, bisekcí či regula falsi. Porovnejte časovou efektivitu metod.

On-line účast na řešení úkolu

Řešit úkol Prohlídka hodnocení úkolu Dotazy,připomínky

Pomocí volby Řešit můžete (po přihlášení) odeslat vaše řešení domácího úkolu (každý úkol smíte řešit jen jednou). Volbou Hodnocení si přečtete hodnocení a komentář od vyučujícího. Dotaz nebo připomínku můžete opakovaně zasílat pomocí tlačítka Dotazy, Komunikace (na levém okraji) zobrazuje příklad možné komunikace s vyučujícím.